Capacitance in parallel

The system of capacitor in parallel is shown in following fig.1

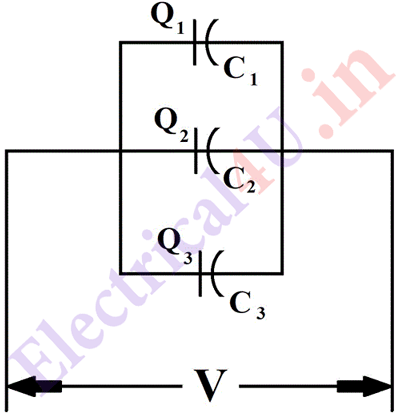
When capacitors are connected in parallel, the potential difference or voltage across each is the same. The total charge is the sum of the charges on each capacitor.

The total charge Q = Q₁ + Q₂ + Q₃

Q₁ = VC₁ ; Q₂ = VC₂ ; Q₃ = VC₃

Q = VC = VC₁ + VC₂ + VC₃

Therefore C = C₁ + C₂ + C₃

Example:- Three capacitors C₁ , C₂ , C₃ of the values of 1μF, 2μF and 4μF are in parallel and connected across a potential of 230 V.
Calculate :- (a) Total capacitance (b) Charge on each capacitor and (c)Total charge.

Solution:- The system of the capacitors in the example is shown in fig. 1
(a) Total capacitance C = C₁ + C₂ + C₃
= 1 + 2 + 4 = 7μF

(b) Charge on capacitor C₁ = VC₁
= 230 x 1 x 10^-6
= 230 x 10^-6 coulomb

Charge on capacitor C₂ = VC₂
= 230 x 2 x 10^-6
= 430 x 10^-6 coulomb

Charge on capacitor C₃ = VC₃
= 230 x 4 x 10^-6
= 930 x 10^-6 coulomb.

(c) The total charge C = VC
= 230 x 7 x 10^-6
= 1610 x 10^-6 coulomb

It may also be checked that Q = Q₁ + Q₂ + Q₃
Q = 10^-6 (230 + 460 + 920)
= 1610 x 10^-6 coulomb