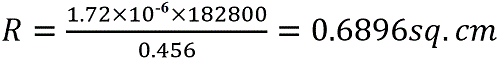Resistance. The resistance of a conductor is that property which opposes the drift of electrons in it. Also under constant conditions the ratio of potential difference to current in the circuit remains constant and this constant is called the resistance of the circuit.
Thus, numerically,

Where V is the potential difference in volts and I is the current in amperes. If both V and I are each equal to unity, then R will also be unity.
In MKS units a conductor has a resistance of one ohm if a potential difference of one volt across it causes a current of one ampere to flow through it.
i.e.

To realize what the resistance is, the Standards Committee called it as an International ohm, and defined it as the resistance of a column of mercury 106.3 cm. long, 1 sq.mm. in cross-section (having a mass of 14:4521 gm.), at the temperature of melting ice.
It has been practically determined that the resistance of a material depends upon the following factors:
(a) It is directly proportional to its length and inversely proportional to its cross-sectional area.
(b) It depends upon the type of material of which the conductor is made of.
(c) It depends upon the working temperature.
(d) It depends upon the purity and hardness of the material,
i.e.

Where is a constant depending on the type of material used and is known as the specific resistance or the resistivity of the material.

Specific Resistance – The resistance of a material is directly proportional to the length and inversely proportional to the cross-sectional area, so
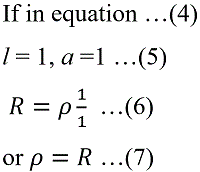
or specific resistance may be defined as the resistance of a material of unit length and of unit cross-sectional area, i.e. the resistance between the opposite faces of a unit cube as represented in Fig.1 If the dimensions of the unit cube are specified in cm. then the unit of specific resistance is ohms per cm. cube. While, if dimensions are represented in inches, the units of specific resistance is per inch cube.

It should be noted that the specific resistance is the resistance of a cm. cube or an inch cube, according to the units utilized, and it is not the resistance per cubic cm. or per cubic inch. Fig.2 represents 4 conductors of same volume, i.e. 1 cubic cm, and their corresponding resistances are as shown.
The specific resistance of an annealed copper wire at 20°C is 0.00000068 ohm per inch cube or 0.00000172 ohm per cm, cube or the resistance of 1 meter length and 1 mm2 in cross-section is (1/58) Ω. It is obvious that the specific resistance is exceedingly small and usually the use of so many zeros is avoided by specifying the resistance in micro ohms or the word micro (μ) is prefixed before ohm represented as μΩ.
1 μΩ = 1 x 10-6 Ω
Hence specific resistance for copper at 20°C
= 0.68 μΩ/inch cube
= 1.72 μΩ/cm. cube
= (1/58) μΩ/m and 1mm2 cross-section
In addition to the above symbol micro the following multiples and sub-multiples are mostly used in electrical engineering:
TABLE 1-2
| Prefix | Meaning | Example |
| Mega (M) | A million (106) | 1MΩ = 100000 Ohm or 106 Ω |
| Kilo (k) | A thousand (103) | 1kΩ = 1000 Ohm or 103 Ω |
| Deci (d) | One-Tenth (1/10) | 1dm = 0.1 Meter or 0.1 m |
| Centi (c) | One-Hundredth (1/100) | 1cm = 0.01 Meter or 10-2 m |
| Milli (m) | One-Thousandth (1/1000) | 1mm = 0.001 Meter or 10-3 m |
| Micro (μ) | One-Millionth (1/1000000) | 1μA = 0.000001 Ampere or 10-6 A |
Example:- Find the resistance of 2000 yards of cable at 20°C, having a diameter of 0:3 inch. Assume the specific resistance of copper at 20°C as 0.72 μΩ-cm.
Solution:-

where p is the specific resistance of the material for 1 cm in length and 1 sq. cm. in cross-section, l is the length in cm. and a is the cross-sectional area in square cm. d2

Ρ at 20oC = 1.72 x 10-6 per cm length and for 1cm. cross section
Therefore