Effective, Virtual, or R.M.S. Value of an Alternating Quantity:_
The question soon arises as to what is to be taken as the effective value of an alternating current relative to a direct current; and since the whole object of producing a current, either direct or alternating, is to transfer energy from one part of the circuit to another, the two currents are compared on an energy basis. Considering the simplest form of energy conversion, it may be said that the effective value of an alternating current is the value of a direct current which produces the same amount of heat in the same time.
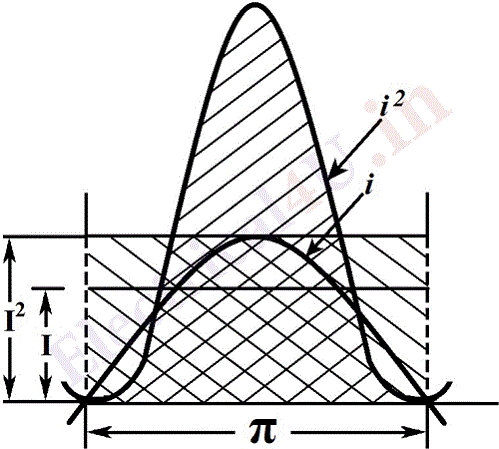
The rate at which energy is converted into heat, i.e. the power (= I2R), is proportional to the (current)2, so that in the case of an alternating current wave the curve obtained by plotting, on the same base, the square of the current at every instant, represents the rate of heat production (fig. 1). The area under the curve then represents the total heat produced, [Since the square of a quantity is always on the positive, the power wave lies wholly on the positive side of the axis. Actually the curve is another sine wave of twice the frequency, and displaced from the current axis by a distance equal to the amplitude.] and since all half waves are similar, only one need be considered. The heat produced by a steady current I in the same time is represented by a rectangle of height I2, so that the effective value of the alternating current is that of the direct current which makes the area of the rectangle equal to the area under the i2 curve. In other words, the height of the rectangle is the mean height of the i2 curve, which can be determined graphically, and is found to be:


Since,
Effective value =√ Mean value of squares
it is often called the root-mean-square (r.m.s.) value: it is also called the virtual value.
The effective, r.m.s. or virtual value of a sinusoidal alternating E.M.F. or current is
(1/√2) Maximum value = 0.707 Maximum value.
Unless the contrary is expressly stated, r.m.s. values are always implied, and represented by capital letters without suffixes.
Mean or Average Value of an Alternating Quantity:_
The average value of an A.C. wave over a whole cycle is obvious zero. Over half a period the average value is given by the mean value of the half wave. This can be determined graphically and is found to be,

The mean or average value of a sinusoidal alternating E.M.F. or current is
(2/π) Maximun value = 0.637 Maximum value.
Form Factor:_
The ratio of r.m.s. value to average value is called the form factor of an alternating wave. For a sine wave,

For non-sinusoidal waves the form factor is greater or less than this value according as the wave is more peaked or flatter than a sine wave. For example, the value for a triangular wave is 1.15 and for a square wave 1.0.
A knowledge of the form factor enables the r.m.s. value to be obtained from the average value, and it is used in the E.M.F. equation of the alternator and transformer.
Vector Representation:_
For many purposes an alternating quantity can be represented more conveniently by means of a rotating vector.
In figure OA is a straight line capable of rotating about O and inclined, at the instant considered, at an angle θ to the horizontal axis OX. If a perpendicular Aa is drawn from A to the vertical axis, Oa, the projection of OA on this axis, is given by:
Oa = OA sin θ
