The effective value of an alternating current for alternating e.m.f. is given by that direct current or e.m.f. which when applied to given circuit for a given time, produces same expenditure of energy as when the alternating current or voltage applied to the same circuit for the same time.
Figure (a) shows an alternating current of any non sinusoidal waveform. Only half the period is shown. Divide the base into n equal intervals which time T/n seconds. Let i1, i2, i3. . . . . in be the mid ordinate in the intervals.

If R is the resistance of the circuit in which the current is flowing, and I is the effective value of the current during the time T seconds, the energy spent I2RT joules. It is also given by T R \frac{\left(i^{2}{ }{1}+i{2}^{2}+i_{3}^{2}+\ldots+i^{2} n\right)}{n}
therefore by equating both expressions,
I=\sqrt{\frac{i_{1}^{2}+i_{2}+i^{2}{ }_{3} \cdots+i^{2} n}{n}} . . .(1)
Thus the effective value of the current is equal to the square root of the mean of the squares of successive ordinates. This value is therefore called the root mean square (r.m.s.) value. Sometimes it is also called virtual value.
AVERAGE AND EFFECTIVE VALUE OF SINUSOIDAL WAVES
Figure (b) shows the plot of one cycle of EMF of sinusoidal waveform.
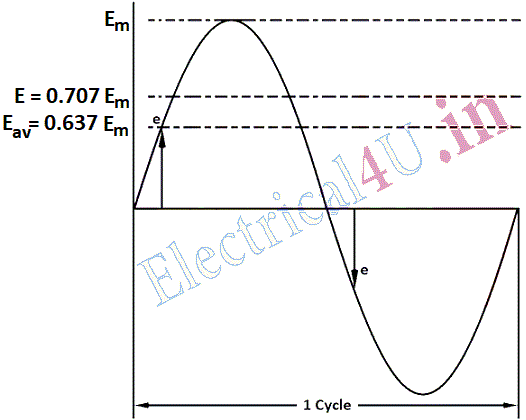
The instantaneous value of e.m.f. e=E_{\max x} \sin \theta where θ=ωt. During a half cycle θ varies between 0 to π radians.
The average value of the e.m.f. over half cycle is given by:
E_{a \sigma}=\frac{1}{\pi} \int_{0}^{\pi} E_{\max } \sin \theta d \theta =-\frac{E_{\max }}{\pi}(\cos \theta)_{0}^{\pi}
E_{a v}=\frac{2}{\pi} E_{\max }=0 \cdot 637 E_{\max } . . .(2)
If the average is taken over the whole cycle, instead of the half cycle, the average value of e.m.f. = 0
If you want to find the effective value or the r.m.s. value of the voltage, let E be the r.m.s. value of the voltage. Integrating the values of e2 over the period 0 to π
E^{2}=\frac{1}{\pi} \int_{0}^{\pi} E^{2} \max \sin ^{2} \theta d \theta
=\frac{E^{2} \max }{2 \pi} \int_{0}^{\pi}(1-\cos 2 \theta) d \theta=\frac{E^{2} \max }{2 \pi}\left[\theta-\frac{1}{2} \sin 2 \theta\right]_{0}^{\pi}
=\frac{1}{2} E^{2} m a xE=\frac{E_{\max }}{\sqrt{2}}=0 \cdot 707 E_{\max } . . .(3)
The effective and average value of voltage are marked in the diagram on the curve.
Form factor : The ratio of effective or RMS value to the average value is termed as form factor.
\text { Form factor }=\frac{E}{E_{a v}} . . .(4)
In case of sinusoidal waveform,
\text { Form factor }=\frac{E_{\max }}{\sqrt{2}} \div \frac{E_{\max }}{\pi / 2}=1 \cdot 11 . . .(5)
Peak factor: Peak factor is defined as the ratio of peak or maximum value to effective or r.m.s. value.
\text { Peak factor }=\frac{E_{\max }}{E} . . .(6)
