Figure. (a) shows the principle of a simple alternator producing alternating voltage. It has two pole generator with the flux passing between the north and the South poles. In the conductor coil when in position no. 1, the rate of change of flux and the EMF produced in it is zero. Assume that the coil is rotated with an angular velocity ω radians/second.
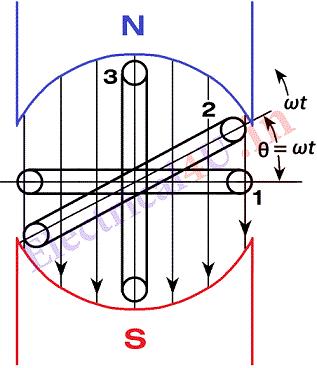
After a time t, it moves through an angle θ = ωt. In this position, the linkages are ɸmax N cosωt where N in the number of turns on the coil. The induced EMF is rate of change of flux linkages.
e=-\frac{d}{d t} \phi_{\max } \mathcal{N} \cos \omega t
=\left(\phi_{\max } \mathcal{N} \omega\right) \sin \omega t
\left(\phi_{\max } \mathcal{N} \omega\right) is the maximum value of the EMF induced,
e=E_{\max } \sin \omega t … (1)
The induced EMF in the conductor and given by alternator is therefore sinusoidal.
In position no. 3 of the coil, it cuts the maximum linkages and the EMF indused in it is maximum. This is obvious as θ = 90o and e=E_{\max }
The case shown is for a simple 2 pole machine. In practice an alternator will have a number of poles and a number of coils suitably connected to obtain the necessary EMF. The number of electrical radians per revolution of a coil on the alternator is 2π times the number of pairs of magnet poles on the machine.
For machine with p poles, the number of cycles per revolution = p/2, if n is the number of revolutions per minute, \frac{n}{60} what is the number of revolutions per second and the frequency is
f=\frac{p}{2} \times \frac{n}{60}=\frac{p n}{120} \text{ cycles/second } … (2)
Radian : An arc of a circle can be expressed as so many degrees of arc or radians of arc.
\text { radius } \times \text { radians of central angle }=\text { length of arc }
r \theta=l \text { or } \theta=\frac{l}{r} … (3)
Where r is the radius, θ is the central angle in radians, and l is the length of arc subtended by two sides forming θ.
From equation (3) , Radian can be defined. An angle formed by two radii of a circle that subtend an arc of the circle equal in length to the radius is one radian.
2 \pi \text { radians }=360^{\circ} \text { or } 1 \text { radian }=\frac{360}{2 \pi}=57 \cdot 3^{\circ}
Frequency is given in terms of cycles per second. It is also sometimes called hertz.
Angular frequency : An angle of 2π radians is passed through every cycle of an alternating quantity.
The angular frequency is therefore \omega=2 \pi f \text { radians/second }
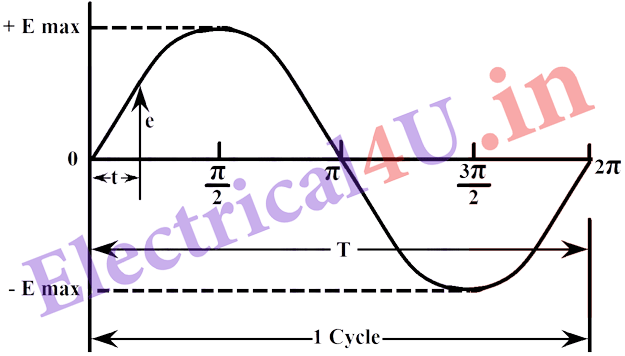
Therefore figure (b) shows e as the instantaneous value of EMF after time t second. E_{\max } is the maximum value of EMF. This occurs when the coil has moved through 90o or\frac{π}{2} electrical radians. Cycle and period T are also marked in the diagram.
